Have you ever heard these phrases when first telling someone that you’re a meteorologist?
"You have the only job in the world where you get paid to be wrong!"
"I consider myself to be an amateur meteorologist!"
and my personal favorite...
"Oh neat, space fascinates me too!"
While meteorologists likely find these statements humorous, it turns out that behind all of these remarks is a common truth; a poor forecast has impacted everyone at least once. Growing up, I had the same viewpoint about meteorologists and weather forecasting. This was largely due to the promise of school closures due to snow that never materialized. Unfortunately, it usually takes only one wrong forecast for people to question their faith in weather forecasting.
So why is it so hard to give an accurate forecast? The answer is really quite complex, so I’ll try to tackle one part of the broader scope of weather forecasting that I’m familiar with: numerical weather forecast modeling.
What is a numerical weather forecast model?
Meteorology is essentially the study of the physics of the atmosphere. Using basic scientific concepts such as Newton's Law of Motion and the Laws of Thermodynamics, the physics behind how the atmosphere works can be represented through a series of equations. If you sprinkle in some fluid dynamics and mathematical methods such as time stepping, you can derive a set of equations that can tell you how the current state of the atmosphere will change into the future.
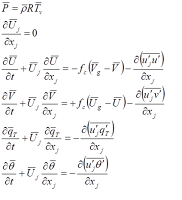 |
| Examples of equations used to represent atmospheric physics (after many approximations) |
So what is the problem you ask? Good question! Let's break down several factors of numerical weather forecast modeling that can lead to an inaccurate forecast.
I. Input data and assimilation
Your weather forecast is only as good as the data you put into it and how you actually get this information into the model. As with many things in life, the phrase "you are what you eat" is as true as ever in weather modeling. One of the statements I made above is that our equations "can tell you how the current state of the atmosphere will change in the future." The key word here is "current state”. In order for our weather model equations to tell us anything useful about the future, we need to first have a good understanding of what the weather is doing right now. To accomplish this, we need to gather as many atmospheric observations as possible. In the U.S., we have one of the largest networks of observations available on the planet that can be used as input data to the forecast model. This network includes (but is not limited to) measurements at the surface, from satellites, weather balloons , radar, aircraft, and even GPS measurements (used for moisture). Many of these measurements are available globally as well.
Using mathematical computer programs, this information is melded together into what is called an analysis. Assuming the measurements all provide quality information (not always a safe assumption!), then what you have is an accurate representation of the current state of the atmosphere. If you live in a densely populated area, you are probably surrounded by a decent amount of measurements. If you don’t, chances are the current state of the weather near you is represented by only a few measurements. This is especially problematic if you live anywhere near rough terrain. You may live several hundred feet up the side of a mountain, and the “measurement” that represents you may be sitting down the slope on the flat surface. In essence, modern weather modeling agencies do their best to generate as accurate an analysis as possible, but even these do not perfectly represent the state of the atmosphere.
The method used to generate an analysis is called data assimilation. I won’t go into detail on this topic, but should mention the techniques applied to data assimilation are often as (if not more) sophisticated that those employed in the weather model itself.
II. Resolution
Once you have your equations and your data, not only do you need an analysis, but you need to determine your model grid. The easiest way to think about a weather model grid is to imagine a box surrounding your state, centered on you. You need to calculate each equation at as many points inside your box as you choose. Do you calculate those equations every few feet, every few kilometers, or more? The more points we choose the higher the model resolution. This is similar to buying a television. The more pixels (points) the TV (model) has, the higher its resolution. If you want to see every detail of every show, you want the highest resolution possible! If you are only interested in a general viewing experience, then perhaps a lower resolution TV works for you. Take a look at the picture below. As we increase the resolution, more and more features become visible. In order to start seeing river valleys, we had to add a significant number of grid points.
 |
| Weather model terrain with increasing resolution (left to right). |
So why not just have more grid points? Going back to our TV example, it is typically true that the better the resolution the higher the cost. This is also true in the weather modeling world. For a weather forecast covering the same region, the higher the resolution the higher the computational cost (more calculations = more computer power).
A decision is therefore needed when running a weather forecast model. Do we want the highest resolution possible, the most area covered, or do we want the forecast to finish as fast as possible? Each decision affects the accuracy of the forecast. If you are running a model that covers the entire planet, there are so many grid points that even if you are using a supercomputer, you still need to determine how high of a resolution you can actually run while still getting a forecast that is useful. After all, what good is a 24-hour forecast, if it takes the computer 25 hours to give it to you?
Just to give some perspective on the impact of resolution, let’s go over an example of a small grid with high resolution. Let’s place a grid that spans 200 kilometers in each of the cardinal directions (N, S, E, and W) from where you are standing. Since we want a high resolution forecast, we will choose to calculation our equations every 1 kilometer. If you have seven equations to calculate, that means you are calculating 7 times 400 times 400 equations (1.12 million). If only it were that easy... you forgot about the atmosphere above you! If you wanted to calculate the same equations every 1 kilometer in the vertical (let say up to 25 kilometers) as well, now you are calculating 7 x 400 x 400 x 25 = 28 million equations. If you wanted a 24-hour forecast, you would need to update the calculation as you move forward in time. For a grid with points 1 kilometer apart, it is common practice to calculate your equations every 6 seconds. This means 7 x 400 x 400 x 25 x 10 (per minute) x 60 (minutes per hour) x 24 (hours per forecast)…that equates to a mere 420 billion calculations! Just for kicks, I ran this example on my quad-core Linux desktop computer. Using all 4 processors, this weather forecast completed in 32 hours. The only benefit to taking this long is that by the time the model run finished, I already had all the data I needed to determine if my forecast was any good! /headslap
 |
| Visual representation of a horizontal grid. Features that exist at the dots must be parameterized. |
III. Parameterizations
In our example above, we learned that running a weather model with a grid spacing of 1km can be very computationally expensive. We must therefore choose to calculate our equations over a coarser grid. But as we move our gridpoints further apart, we begin to lose resolution and the atmospheric features that we can forecast decrease. For example, a typical supercell thunderstorm is about 10 kilometers wide. If our grid points are spaced 20 kilometers apart, this means the entire thunderstorm can exist inside our grid and never actually touch a single grid point. So how exactly can we forecast such an event? We have 2 choices here: we can either increase our resolution so we have more grid points, or we can use what is called a parameterization. Since we already know the limitations of increasing the resolution, let’s talk about parameterizations. If we consider the example of the thunderstorm again, a parameterization will tell each of the four grid points surrounding the storm how that storm is impacting them. While we lose the majority of the details of the storm itself, we can still extract valuable information about how that storm may be impacting the forecast as a whole .
Since we can't run our weather models at as high a resolution as we would like, parameterizations are necessary. The trade-off is that we are losing detailed information. With that said, I should also mention that many of the weather models available today were never designed to run at very high resolutions, and therefore one cannot expect that many grid points covering a storm will lead to an accurate forecast of its evolution.
IV. Representativeness
If you happen to live directly on top of a co-located weather model grid point, then you can expect a pretty good forecast. Chances are that the grid point closest to you is actually not perfectly representative of where you live. This is true in weather models and also in weather observations. A classic example is when you look up the current weather conditions for Denver, CO. Many weather applications are going to show you the readings from Denver International Airport (DIA). For anyone that has ever been to DIA, some 20km northeast of the downtown area, you can attest that the airport does not represent the weather in downtown Denver very well.
The problem of representativeness is particularly prevalent in areas with varying terrain. If you live in a valley, or near water, you are probably aware that a 1 kilometer walk in a particular direction can put you outside of the valley or even in the water! This means if your weather model doesn't represent your particular area very well, it may think you actually live under water!
V. Approximations
This may be a little too deep for this conversation, but in the interest of being complete I will mention the concept of approximations. When developing the equations we use to represent atmospheric physics, we often make approximations to simplify those equations. This is widely accepted and generally not problematic, but it does lead to tiny errors in our math. The problem with errors is that when you perform billions of calculations, tiny numbers start to add up. As our forecast moves further and further out in time, the probability that our errors are impacting the forecast increases dramatically. As you get to a week or more out into the future, the change in temperature on a given day can actually be as large as the errors inside of a weather model .
VI. Chaos
The topic of chaos is definitely too deep for this conversation, but I do want to bring up the concept and point the interested reader to a book on the subject. The theory of chaos basically states that small differences in initial conditions (see the 'you are what you eat' discussion above) yield widely diverging outcomes. For dynamical systems such as atmospheric flow, these diverging outcomes make long-term prediction problematic (to say the least). The book I mentioned above can be found here .
I hope you now have a better appreciation for the complexities behind generating a weather forecast. There has been much discussion recently surrounding the quality of weather forecast models. While it is true that some forecast models outperform others, it must be said that all models suffer from the problems described in this post. Numerical weather prediction models have seen drastic improvements over the past few decades and the future is bright for continued improvements to our science.
The next time you hear an ‘amateur meteorologist’ who thinks ‘space is fascinating too’ complaining about a blown forecast, just remember that any one or perhaps all of the factors described above could have led to it. That isn't to say your local meteorologist is perfect, but given what you now know about forecast models, they may deserve the benefit of the doubt, even if they are getting paid to be wrong .
Cheers.
SM


